خرید دیجی کالا با تخفیف در صورت کلیک از اینجا 

درس دکترای مدیریت - برنامه ریزی غیرخطی

برنامه ریزی غیرخط درس دکترای مدیریت - برنامه ریزی غیرخ

مقدمه

از آنجا که برنامه ریزی خطی را می‌توان شالوده تحقیق در عملیات دانست، بسیاری از مباحث تحقیق در عملیات با آن سروکار دارد. فرض اصلی برنامه ریزی خطی این است که همه توابع (اعم از تابع هدف یا محدودیت ها) خطی باشند. اگر چه این فرض در بسیاری از مسائل واقعی برقرار است لیکن در موارد زیادی هم صادق نیست.

هدف مسائل برنامه ریزی غیرخطی در شکل کلی آن، پیدا کردن مقادیر(x=(x₁,x₂,…,x_n است به طوریکه :

که (f(x و (g_i(x توابعی معلوم از n  متغیر تصمیم هستند.

نکته: در این درس برای راحتی فرض می‌شود که کلیه توابع مشتق پذیر هستند.

الگوریتمی وجود ندارد که بتواند همه مسائلی که در چارچوب برنامه ریزی غیرخطی به صورت فوق می‌گنجد را حل کنند. لیکن، چنانچه فرضیات مشخصی در مورد این توابع به کار گرفته شود، آن گاه حالت‌های خاصی از برنامه ریزی غیرخطی بدست می‌آیند که در رابطه با حل آن‌های پیشرفت‌های چشمگیری حاصل شده است. در این درس، ابتدا چند نمونه از کاربرد برنامه ریزی غیرخطی و سپس اصول و مفاهیم اساسی حل برخی از انواع مهم مسائل آن ارایه می‌گردد.

مسئله حمل و نقل با تخفیف هزینه حمل نسبت به میزان بار

همان طور که در درس ۵ گروه آموزشی بهینه یاب گفته شد با معلوم بودن میزان عرضه و تقاضا، هدف مسئله حمل و نقل تعیین برنامه بهینه حمل کالا از مبادی گوناگون به مقصدهای مختلف است، به طوری که کل هزینه‌ها کمینه شود. در آن جا فرض بر این بود که هزینه حمل هر واحد کالا بین هر مبدا و مقصد مشخص، صرفنظر از میزانی که حمل می‌شود مقداری ثابت باشد. در عمل، ممکن است این هزینه ثابت نبوده و برای محموله‌های بزرگ تخفیف‌هایی منظور گردد، به طوری که هزینه نهایی حمل یک واحد دیگر کالا، شبیه شکل زیر باشد. هزینه حمل x واحد محصول به صورت تابع غیرخطی (C(x از نوع تابع خطی شکسته یا Piece-wise linear function است.

بنابراین، در صورتی که چنین فرضی در مورد هر مبدا و مقصد صدف نماید، یعنی هزینه حمل x_ij  واحد از مبدا i (به ازای i=1,2,…,m) به مقصد  (j (j=1,2,…,n برابر (C_ij(x_ij باشد، آنگاه تابع هدف به شکل زیر در می‌آید.

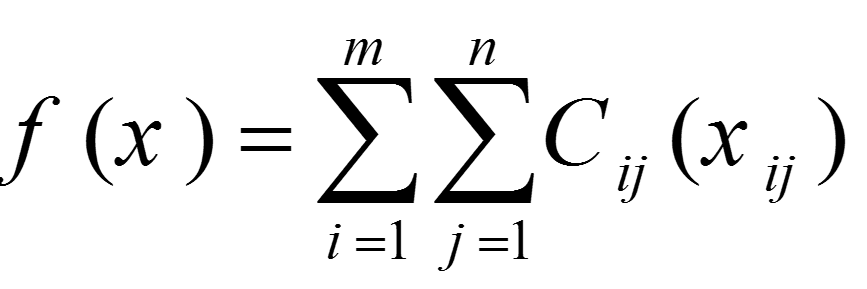
با این وجود، در چنین مسائلی حتی اگر تابع هدف هم غیرخطی باشد، محدودیت‌ها عموما دارای ساختار ویژه ای هستند که همچنان در چارچوب مدل حمل و نقل خطی فرموله می‌شوند.

انتخاب ترکیب سرمایه گذاری با بازده قطعی

امروزه جهت انتخاب گزینه‌های مناسب برای سرمایه گذاری، مدل‌های کامپیوتری که بر مبنای برنامه ریزی غیرخطی پایه گذاری شده اند به صورت ابزاری متداول در خدمت مدیران حرفه ای بازار بورس سهام درآمده اند. از آن جایی که سرمایه گذاران به دو عامل، یعنی میزان بازدهی سرمایه گذاری‌ها و همچنین خطرهایی که در بطن آن‌ها وجود دارد اهمیت می دهند، لذا ترکیب سرمایه گذاری باید طوری انتخاب شود که تحت شرایط موجود، بین بازده سرمایه و خطری که متوجه آن است رابطه بهینه ای برقرار باشد.

در مورد چنین مسئله ای، مدل برنامه ریزی غیرخطی به شکل زیر بیان می‌شود:

فرض کنید که خرید n نوع سهام مختلف تحت بررسی است و متغیر تصمیم x_j   معرف تعداد سهام نوع j است که انتخاب می‌شود (به ازای j=1,2,…,n). چنانچه µ_j و δ_jj به ترتیب بیانگر میانگین و انحراف معیار بازده یک عدد از نوع سهام نوع j باشند و  δ_jj  معرف میزان خطر در این سرمایه گذاری است. لذا میانگین (R(x و واریانس (V(x کل بازده سرمایه گذاری، به شرح زیر بدست می‌آید.

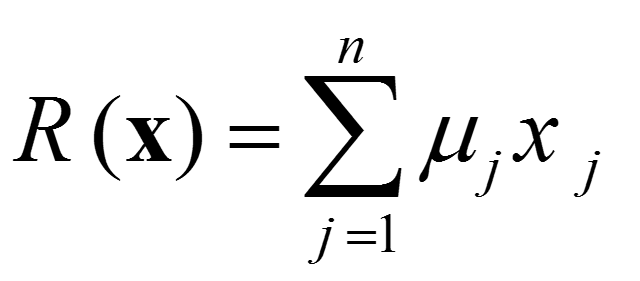
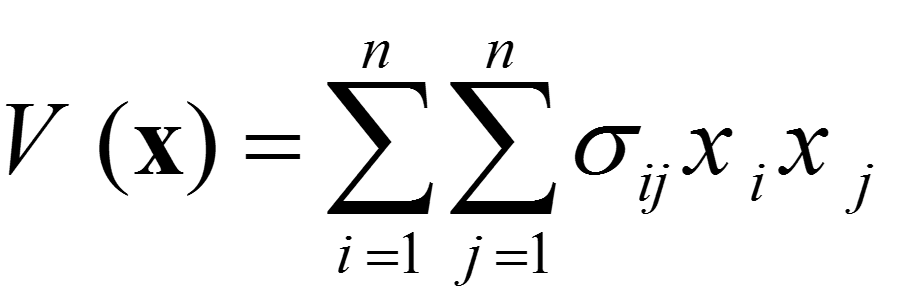
که در روابط بالا، (V(x معیار سنجش خطر مجموع سرمایه گذاری‌ها است. تبادل بهینه بین دو عامل فوق، از طریق ترکیب نمودن آن‌ها در تابع هدف به صورت زیر انجام می‌گیرد.

در تابع هدف فوق که باید حداکثر شود، عدد غیرمنفی β بیانگر میزان مطلوب تبادل بین بازده و خطر سرمایه از دید سرمایه گذار است. معنای ۰=β این است که خطر سرمایه گذاری مطرح نیست و انتخاب مقدار بزرگ برای β به معنای اهمیت دادن زیاد به خطرناک بودن سرمایه گذاری خواهد بود.

مدل کامل برنامه ریزی غیرخطی این مسئله به صورت زیر در می‌آید.

که P_i بیانگر  قیمت یک عدد از سهم نوع i و B کل بودجه ای است که برای سرمایه گذاری در نظر گرفته شده است و تابع هدف، همان امید ریاضی مطلوبیت سرمایه گذاری است که در مدل فوق به دنبال بیشینه کردن آن هستیم.

بیان ترسیمی مسایل برنامه ریزی غیرخطی

در صورتیکه مسئله برنامه ریزی غیرخطی دارای فقط یک یا دو متغیر باشد، می‌توان آن را با روش ترسیمی حل کرد. مثال زیر را در نظر بگیرید.امه ریزی غیرخطی و ارایه دستورهای حل

مثال: یک شرکت تولیدی درب و پنچره، داراه سه کارگاه است. در کارگاه ۱ قاب‌های آلومینیومی و قسمت‌های فلزی تولید می‌شود. در کارگاه ۲، قاب‌های چوبی تولید می شود و در کارگاه ۳، برش شیشه و سوار کردن آن به قاب‌ها آنجام می‌شود. مدیریت این کارگاه‌ها به دنبال تولید دو محصول جدید هستند و از مرکز تحقیق در عملیات خواسته اند که میزان تولید از هر محصول را با توجه به ظرفیت کارگاه چند واحد است. محصول ۱، دری با قابی آلومینومی و محصول ۲ پنجره‌ای شیشه با قاب چوبی است. با توجه به این که هر دو محصول برای جوشکاری نیاز به کارگاه ۳ دارد، ظرفیت این گارگاه باعث می‌شود که رقابتی بین این دو محصول ایجاد شود. در جدول زیر سود هر محصول، میزان استفاده از منابع و ظرفیت هر کارگاه آورده شده است.

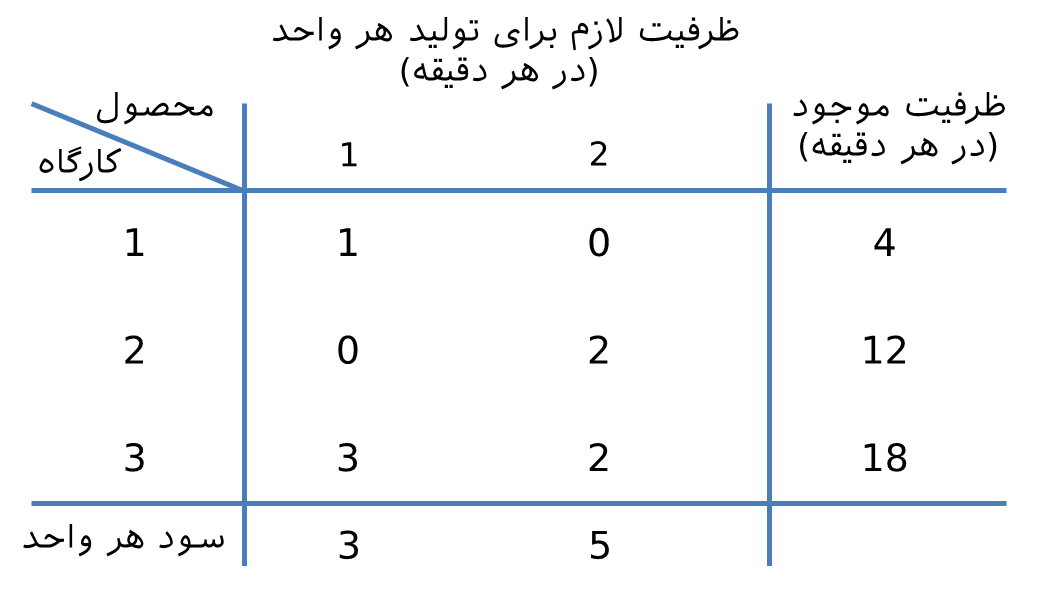
x₁ و x₂ به ترتیب تعداد محصولات ۱ و ۲ در هر دقیقه است و z نشان دهنده سود حاصل از فروش در هر دقیقه است. در ادبیات تحقیق در عملیات به x₁ و x₂  متغیرهای تصمیم‌گیری (decision variables) و z را تابع هدف (objective function) گفته می‌شود.

برای تولید هر واحد محصول ۱، یک واحد از کارگاه ۱ مصرف می‌شود که در هر دقیقه کارگاه ۱ تنها چهار واحد ظرفیت برای محصول جدید موجود دارد. این محدودیت به صورت جبری ۴≥x₁ نمایش داده می‌شود. به طور مشابه برای کارگاه شماره ۲، محدودیت ۱۲≥۲x₂  برای محصول ۲ مورد نیاز است. ظرفیت کارگاه ۳ توسط هر دو محصول استفاده می‌شود که باعث محدودیت ۱۸≥۲x₂+3x₁ می‌شود. چون محصول‌ها نمی‌توانند منفی باشند، متغیرهای تصمیم‌گیری نامنفی هستند و نمایش ریاضی آن به صورت  ۰≤x₂ و ۰≤x₁ می‌شود. به طور خلاصه نمایش ریاضی مدل برنامه‌ریزی خطی این مسئله به صورت زیر می‌شود.

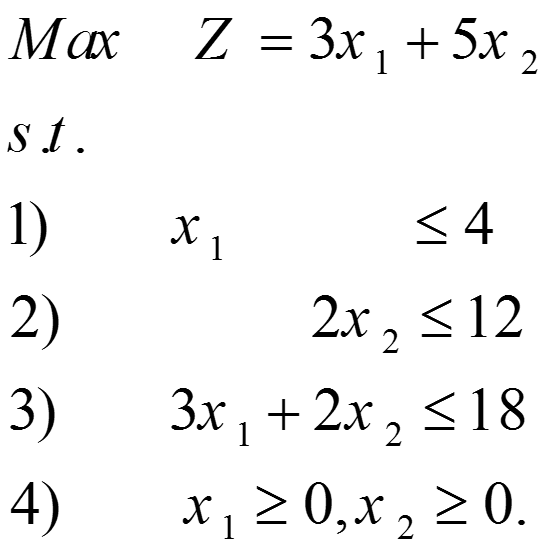
به دلیل این که این مدل برنامه‌ریزی خطی شامل تنها دو متغیر  x₁ و x₂ است، می‌توان برای حل آن از روش ترسیمی بهره برد. این شیوه مستلزم رسم یک شکل با محورهای  x₁ و x₂ است. هر یک از محدودیت‌ها بخشی از محور دوبعدی را پوشش می‌دهد که از اشتراک این محدودیت‌ها، فضای موجه یا امکان پذیر مسئله ایجاد می‌شود. ما به دنبال نقطه‌ای هستیم که بیشترین مقدار عبارت z را ایجاد می‌کند.

شکل زیر نمایش هندسی مدل این مسئله را نشان می دهد با این تفاوت که محدودیت‌های ۲ و ۳ با محدودیت زیر جایگزین شده است.

در شکل زیر مشخص است که جواب بهینه برابر با (۲,۶)=(x₁,x₂) خواهد بود.

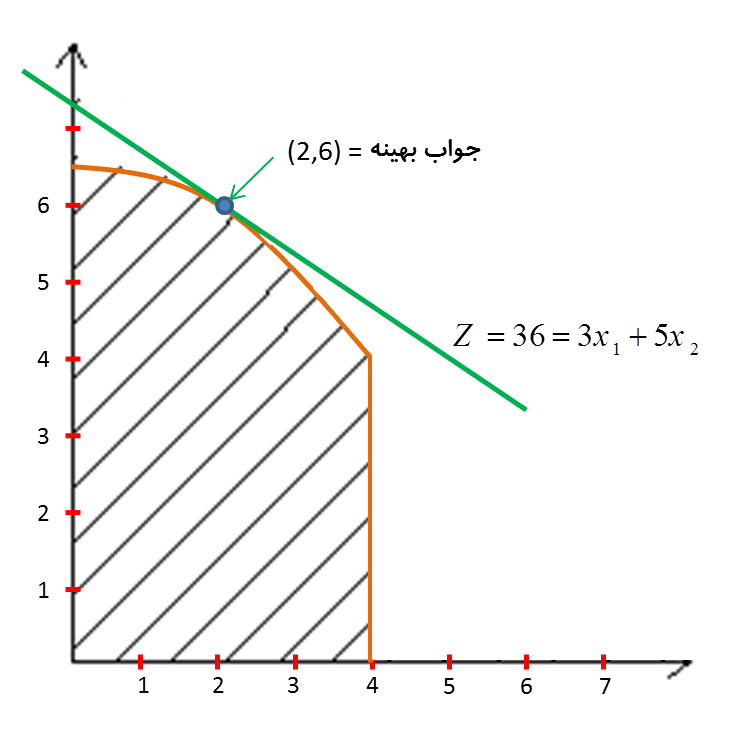
به علاوه، جواب همچنان روی مرز منطقه موجه قرار می‌گیرد. لیکن یک جواب گوشه موجه نیست. چنانچه تابع هدف نیز تغییر کرده بود (مثلا  Z=3x₁+x₂)، آنگاه جواب بهینه می‌توانست بر یک جواب گوشه موجه منطق باشد. اما به هر حال، این واقعیت که جواب بهینه لزوما در یک گوشه قرار ندارد به معنای آن است که نتیجه بسیار مهمی که در برنامه ریزی خطی مورد استفاده قرار می‌گرفت، یعنی فقط جستجوی جواب‌های گوشه موجه، دیگر در مورد برنامه ریزی غیرخطی کارسازی نیست.

حال فرض کنید که محدودیت خطی مثال فوق همچنان در مسئله باقی باشند، اما تابع هدف غیرخطی گردد. برای نمونه، اگر Z=126x₁-9x₁²+182x₂-13x₂² باشد. در این صورت بیان ترسیمی مسئله به صورت شکل زیر و جواب بهینه آن x₁=5 و x₁=2.666 خواهد بود. این جواب هم روی مرز منطقه موجه قرار می‌گیرد.

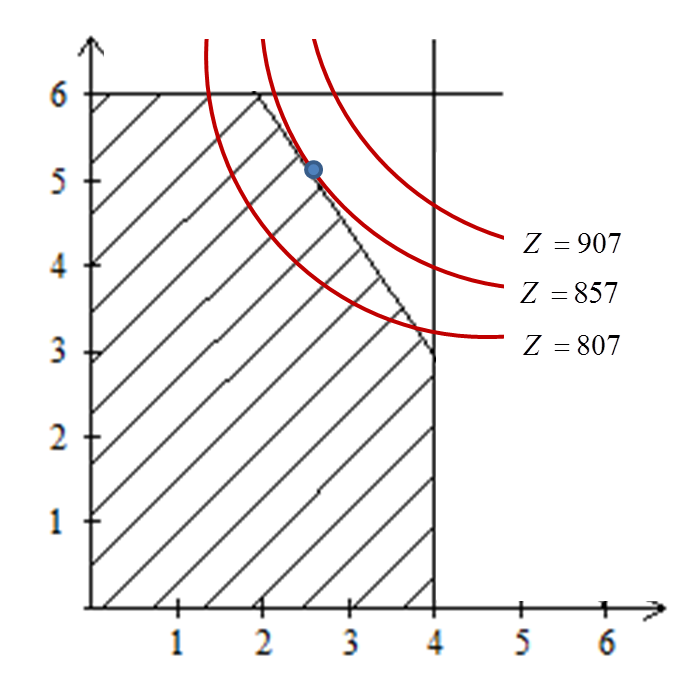
از این رو یک الگوریتم عمومی و کلی برای این نوع مسائل، نمی‌تواند تنها به جواب‌های حدی بپردازد، بلکه باید تمام جواب‌های داخلی را بررسی نماید.

پیچیدگی دیگری که در مسائل برنامه ریزی غیرخطی ظاهر می‌شود این است که یک جواب حداکثر نسبی لزوما یک جواب حداکثر مطلق نیست. برای نمونه، تابع یک متغیره ای که در شکل زیر ترسیم شده است را در نظر بگیرید.

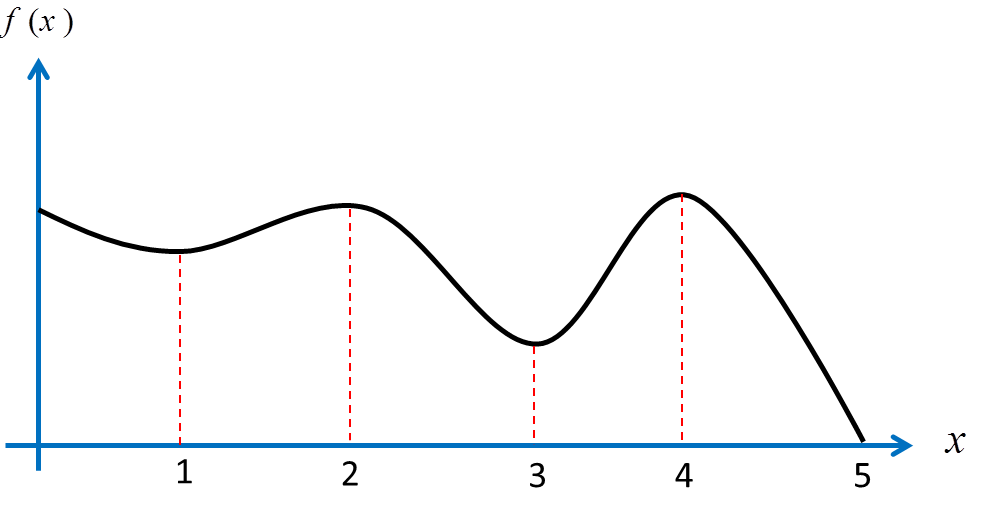
این تابع در فاصله بین ۰ تا ۵سه حداکثر نسبی یعنی x=0 و x=2 و x=4 دارد، در حالی که فقط یکی از آن‌ها یعنی x=4 جواب حداکثر مطلق است. به همین ترتیب تابع دارای سه حداقل نسبی x=1,3,5 و فقط یک حداقل مطلق x=4 است.

از آنجا که الگوریتم‌های برنامه ریزی غیرخطی تنها می‌توانند جواب‌های حداکثر نسبی (حداقل نسبی) را بدست آورند. لذا آگاهی از این که یک جواب حداکثر نسبی تحت چه شرایطی، حداکثر مطلق نیز خواهد بود اهمیت زیادی دارد. یادآوری می‌شود که در مورد تابع یک متغیری و بدون محدودیت (f(x (با فرض داشتن مشتق‌های اول و دوم)، برای اثبات این که جواب حداکثر نسبی همان حداکثر مطلق است، کافی است که رابطه زیر برقرار باشد.

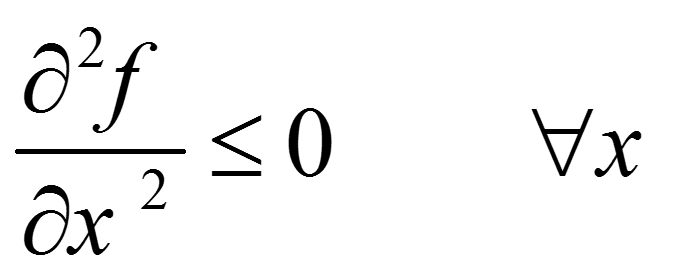
چنین تابعی که خمیدگی آن همیشه به سمت پایین است تابع مقعر یا Concave function نامیده می‌شود. به همین ترتیب، اگر علامت ≤ را با ≥ جایگزین کنیم، به تابع حاصل که خمیدگی آن همیشه به طرف بالا است تابع محدب یا Convex function می‌گویند.

وقتی یک مسئله برنامه ریزی غیرخطی محدودیتی ندارد، مقعر بودن تابع هدف تضمین می‌کند که هر جواب حداکثر نسبی یک جواب حداکثر مطلق باشد. به طور مشابه محدب بودن تابع برای حداقل مطلق بودن هر جواب حداقل نسبی کفایت می‌کند.